
- Автор Stanley Ellington [email protected].
- Public 2023-12-16 00:22.
- Последнее изменение 2025-01-22 16:12.
Простая линейная регрессия - это статистический метод, который позволяет нам суммировать и изучать отношения между двумя непрерывными (количественными) переменными: другая переменная, обозначенная y, рассматривается как ответ, результат или зависимая переменная.
Также спросили, что такое простой пример линейной регрессии?
Линейная регрессия количественно определяет взаимосвязь между одной или несколькими переменными-предикторами и одной переменной результата. Для пример , линейная регрессия может использоваться для количественной оценки относительного влияния возраста, пола и диеты (переменные-предикторы) на рост (переменная результата).
как рассчитать простую линейную регрессию? В Уравнение линейной регрессии В уравнение имеет вид Y = a + bX, где Y - зависимая переменная (то есть переменная, которая идет по оси Y), X - независимая переменная (т.е. она нанесена на ось X), b - наклон линии а - точка пересечения по оси y.
Точно так же вы можете спросить, какова цель простой линейной регрессии?
Простая линейная регрессия похожа на корреляцию в том, что цель состоит в том, чтобы измерить, в какой степени линейный связь между двумя переменными. В частности, цель из линейная регрессия заключается в том, чтобы «предсказать» значение зависимой переменной на основе значений одной или нескольких независимых переменных.
Как сделать шаг за шагом линейную регрессию?
Первое шаг позволяет исследователю сформулировать модель, т.е. что переменная X оказывает причинное влияние на переменную Y, и что их взаимосвязь линейный . Секунда шаг из регресс анализ должен соответствовать регресс линия. Математически оценка методом наименьших квадратов используется для минимизации необъяснимой невязки.
Рекомендуемые:
Что такое Python с линейной регрессией?
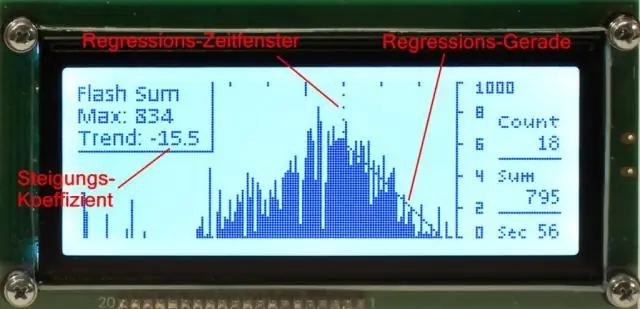
Линейная регрессия (реализация Python) Линейная регрессия - это статистический подход для моделирования отношений между зависимой переменной с заданным набором независимых переменных. Примечание: в этой статье мы называем зависимые переменные откликом, а независимые переменные - функциями для простоты
Как выбрать лучшую модель множественной регрессии?

При выборе линейной модели следует учитывать следующие факторы: сравнивайте линейные модели только для одного и того же набора данных. Найдите модель с высоко настроенным R2. Убедитесь, что эта модель имеет одинаково распределенные остатки около нуля. Убедитесь, что ошибки этой модели находятся в пределах небольшой полосы пропускания
Что такое модель второго порядка в регрессии?
Модель представляет собой просто общую модель линейной регрессии с k предикторами, возведенными в степень i, где i = от 1 до k. Полином второго порядка (k = 2) образует квадратичное выражение (параболическая кривая), полином третьего порядка (k = 3) образует кубическое выражение, а полином четвертого порядка (k = 4) образует выражение четвертой степени
Какие предположения делает алгоритм машинного обучения линейной регрессии?

Предположения относительно оценок: независимые переменные измеряются без ошибок. Независимые переменные линейно независимы друг от друга, т.е. в данных отсутствует мультиколлинеарность
Что такое полная модель в регрессии?

Как вы правильно догадались, в контексте множественной линейной регрессии с предикторами X1,…, Xp и откликом Y полная (или неограниченная) модель представляет собой обычную оценку OLS, где мы не накладываем никаких ограничений на коэффициенты регрессии различных предикторов
